pn接合が熱平衡状態に達するまで

pn接合が熱平衡状態に達するまでの様子を説明した。
\(n_i\) : 真性半導体密度, \(N_A\) : p型半導体の不純物濃度, \(N_D\) : n型半導体の不純物濃度, \(k\) : ボルツマン定数, \(T\) : 絶対温度

p型半導体とn型半導体が接触させてpn接合を作る(実際にはn型基板にp型の不純物イオンを注入して製造する)。
p型とn型を接触させたときの時刻を\(t = 0 (s)\)とする。
電子による電流\(J_n(x, t)\)は次のように表される(1次元系)。
$$J_n(x, t) = q\mu_nn\mathcal{E_x}\,+ qD_n\frac{dn}{dx} \tag{1}$$
ホールによる電流\(J_p(x, t)\)は次のように表される
$$J_p(x, t) = q\mu_pp\mathcal{E_x}\,- qD_p\frac{dp}{dx} \tag{2}$$
右向きを\(x\)の正の方向としている。
右辺の第1項はオームの法則で表される電界によるドリフト電流、第2項はキャリアの濃度差に起因する拡散電流である。\(t = 0 (s)\)のとき、\(\mathcal{E_x}=0\)とする(電場の存在しない状況でp型とn型を接触させてpn接合を作り始めた)。
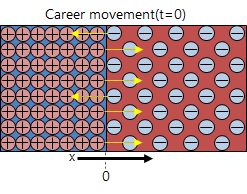
　\(t = 0 (s)\)のとき、
電場は存在せず、キャリアが濃度の濃い側から濃度の薄い側に拡散する((1), (2)式の右辺第1項は0で第2項のみで電流が流れる)。そして空乏層が広がっていく。

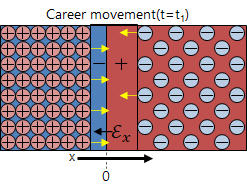
　\(t = t_1 (s)\)のとき(拡散電流よりもドリフト電流が小さいとき)、
キャリアが移動したのでp型のアクセプターイオン(負の電荷)とn型のドナーイオン(正の電荷)による電場(\(\mathcal{E_{x1}}\))が発生する下図に示すように\(x\)の負の向きの電場である。

このとき、電子電流とホール電流は次のようになる。電場の\(x\)方向に対する符号を明確にするために絶対値記号を用いて表した。
$$J_n(x, t_1) = -q\mu_nn|\mathcal{E_{x}(x, t_1)}|+ qD_n\left|\frac{dn}{dx}(x, t_1)\right| \tag{3}$$
$$J_p(x, t_1) = -q\mu_pp|\mathcal{E_{x}(x, t_1)}| + qD_p\left|\frac{dp}{dx}(x, t_1)\right| \tag{4}$$
今、第1項よりも第2項の方が大きいと仮定しているので、電流は\(x\)の正の方向に流れている。このため、空乏層はまだ広がり続ける。
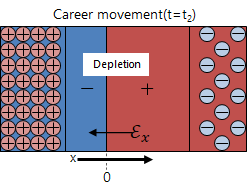
　\(t = t_2 (s)\)のとき(拡散電流とドリフト電流が釣り合って熱平衡状態に達したとき)、
空乏層の拡張が止まる。

このとき、下記の式が成り立つ
$$J_n(x, t_2) = -q\mu_nn|\mathcal{E_{x}(x, t_2)}|+ qD_n\left|\frac{dn}{dx}(x, t_2)\right| = 0 \tag{5}$$
$$\Rightarrow \mu_nn|\mathcal{E_{x}(x, t_2)}| = D_n\left|\frac{dn}{dx}(x, t_2)\right| \tag{6}$$
アインシュタインの関係式\(D_n = \frac{\mu_nk_BT}{q}\)を用いれば
$$qn|\mathcal{E_{x}(x, t_2)}| = k_BT\left|\frac{dn}{dx}(x, t_2)\right| \tag{7}$$
同様に
$$\mu_pp|\mathcal{E_{x}(x, t_2)}| = D_p\left|\frac{dp}{dx}(x, t_2)\right| \tag{8}$$
$$qp|\mathcal{E_{x}(x, t_2)}| = k_BT\left|\frac{dp}{dx}(x, t_2)\right| \tag{9}$$
ここで注意したいのは、一つ一つのキャリアが発生した電場によって止まっているわけではないということだ。
一つ一つのキャリアキャリアは動いているが、ドリフト電流と拡散電流が釣り合っているため、
正味の電流は0になっているように見えるのだ。

参考にした文献
1. Device Electronics for Integrated Circuits, 3ed